倭人伝の距離は「ピタゴラスの定理」でつくられた
みどころ ●　倭人伝の「里」は当時魏で用いられていた１里＝４３５㍍でなく、１里＝７０～１００㍍程度の「短里」だとする説が多いが、「短里」などというものは存在しない。 ●　倭人伝の距離は陳寿が「ピタゴラスの定理」で　３：４：５　になるようにつくったもので、実距離とは関係がない。 ●　韓国の方４千里は、郡から狗邪韓国７千里から「ピタゴラスの定理」でつくったものです。 ●　末盧国から伊都国への「東南」「陸行」は地図（観念）上のことで、実際とは関係ない。
倭人伝の距離は実距離ではない ●　距離に関する説は二つに大別できる　①　郡使の出張報告に基づく実際の距離だとする説　②　陰陽五行説などに基づいてつくられた観念上の距離だとする説 ●　わたしは「つくられたもの」と考えています。「つくられた距離」だとする理由 ●　国の地形が方形とされ、実際の地形は考慮されていない。　①対馬国＝方４００里、壱岐国＝方３００里とありますが、対馬島は南北７０キロ。巾１６キロ、４：１の細長い地形です。　②対馬島と壱岐島の大きさの比率も実際は４：１です。 ●「里」の長さが統一されていない。　①末盧国は唐津市、伊都国は前原市、奴国は春日市に比定されます。　②　唐津市～前原市は２５キロ、と前原市～春日市は３０キロです。　③　末盧国～伊都国５００里一里＝５０㍍、、伊都国～奴国１００里、一里＝３００㍍の説明ができません。　④伊都国は郡使が滞在したところです。その両隣の距離測定に６倍もの大きな差が出るはずはありません。 ●韓国は南北４００キロで方４千里だから一里＝１００㍍。　①　壱岐国は一辺１６キロの方形を方３００里だから一里＝５３㍍。　②　壱岐国～末盧国の千里は５０～６０キロなので一里＝５０～６０㍍。 ●「短里」という尺度が存在したのであれば呼称を変えるはず。　　同じ「里」という呼称を用いて異なる長さを表すことはあり得ません。 ●「短里」が東夷あるいは倭で用いられた尺度単位だとする説もあります。　　自国文化に誇りを持つ中国官人が公式記録の中で東夷の単位を用いることもあり得ません。 ●「１万２千余里」は実際の距離とは考えられません。「遠い距離」を表現する虚数だと考えます。　①『魏志』東夷伝の「鮮卑伝」の記事につぎのようにあります。　　　・【檀石槐は、元の凶奴の土地をまるまる我がものとし、東西１万２千里、南北は７千里にわたって、手中に収めた】　②『漢書』西域伝の記事です。　　　・大宛国。長安を去ること１万２千５百５０里　　　・烏弋山離国。長安を去ること１万２千２００里　　　・安息国。長安を去ること１万１千６００里　　　・大月氏国。長安を去ること１万１千６００里　　　・康居国。長安を去ること１万２千３００里 ●　距離の組み合わせが３：４：５となること。このような数字はつくられていることが多い（詳細後述）。
「距離」はどのようにつくられたのか　陰陽五行説による創作ではない ●　松本清張氏は、「１万２千余里」は単に朝貢する外国との「遠い距離」を表現する虚数だとしています。 ●　そのほかの倭人伝にある距離も陳寿が陰陽五行説によって机上で創作した虚妄の数字だとしています。　①　そのような距離ならば、なぜつくってまで記載したのかという説明が必要です。　②　陰陽五行説は数字をつくる手段に過ぎず、つくった目的ではありません。　③　東夷伝全体に距離が記載され、倭国だけ距離がわからないので陰陽五行説によってつくったというのなら話の筋が通ります。しかし、　距離の書かれているのは倭人伝だけなのです。 ●　倭人伝の距離問題は、なぜ倭人伝にだけ距離か書かれたのかも重要なのです。　新説：「ピタゴラスの定理」による創作説　 ●　陰陽五行説では３、５、７などの数字を使いますが、各数字を関連づけることはありません。 ●　倭人伝の数字は３：４：５とセットでつくられています。下図をご覧ください。この３：４：５は陰陽五行説から出たものではありません。「ピタゴラスの定理」の３：４：５なのです。
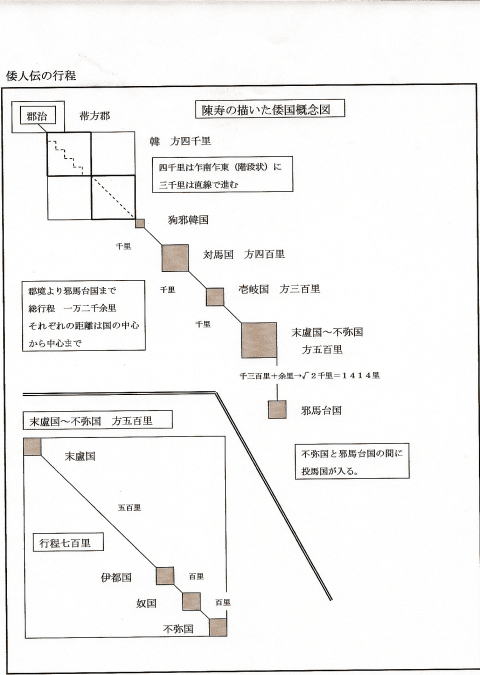
●　下記の倭人伝行程図は、倭人伝の記載を基にわたしがつくりました。 ●　陳寿もこのような地図をつくっていたと考えました。

①　【自郡至女王国万二千余里】の１万２千が３＋４＋５です。　②　１万２千里は狗邪韓国までの７千里と倭の５千里となります。　③　７千里は３千里＋４千里で、倭の周旋５千里につながり、３：４：５になります。　④　韓国の方４千里、倭地の周旋５千里、大海の３千里の組み合わせは３：４：５です。　　　　韓伝には方４千里以外距離は記載されません。郡から倭に行く道が韓国を通るので、方４千里を作ったのです。　⑤　壱岐国の方３００里、対馬国の方４００里とありますが、方５００里が見当たりません。　方５００里は末盧国・伊都国・奴国・不弥国の４ヵ国をまとめて一つの範囲として陳寿がつくりました。　⑥　②で述べたように狗邪韓国までの七千里は３＋４ですが、韓の方４千里はこの７千里からつくられました。　７千里を３：４に分け３千里は直線の道、４千里は碁盤目のジグザグ道とし、それぞれを対角線とする方形をつくります。 ●　ピタゴラスの定理で計算すれば、前者が方２千１００里、後者が方２千里となります。この二つを合わせた４千１００里を韓の方四千里としたのです（詳細後述）。　陳寿とピタゴラスの定理 ●「ピタゴラスの定理」は中国最古の数学書『九章算術』に載っています。陳寿は三世紀後半の人ですから「定理」を習得していてもおかしくありません。 ●『九章算術』は周から前漢時代に解かれた数学問題を紀元前二世紀から後一世紀ころに集成した書です。 ●　その第九章に勾股術として「ピタゴラスの定理」に関する問答が２０ほど載っています。　　・今有勾三尺、股四尺、問為弦幾何。答曰五尺】（問：短辺３メートル、長辺４メートルなら、斜辺は？答：５メートル）　　・【勾股各自乗、并、而開方除之、即弦】（短辺と長辺の自乗の和は斜辺の自乗に等しい）　　　（勾＝鉤は直角三角形の短辺、股は長辺、弦は斜辺） ●　倭人伝の距離にピタゴラスの定理を知らなければつくり出せない数字を用いていることなどから、『九章算術』にある鉤股術をマスターしていたことは疑いありません。
３：４：５の詳細説明　倭の周旋５千里 ●『後漢書』は邪馬台国までの距離を１万２千里と記しますが、女王国が最遠とはしていません。倭人伝は邪馬台国を女王国の南界として周旋５千里としています。５千里という数字がほしかったのです。 ●　また倭の５千里を海路３千里と陸路２千里としたのも韓の地と倭の地の間に大海３千里をつくりたかったのです。 ●　そして倭の周旋５千里と大海３千里に韓の方４千里を組み合わせて３：４：５をつくりました。　韓の方４千里は狗邪韓国までの７千里から　 ●　韓伝には方４千里以外距離は記載されません。郡から倭に行く道が韓国を通るので、方４千里を作ったのです。 ●　倭人伝は帯方郡から狗邪韓国までの道のりを７千里とします。これは韓国の西と南の海岸を航行する距離だというのが定説になっていますが、韓国は方４千里です。４千里の二辺を行けば８千里になります。 ●　陳寿は郡からみた倭国の位置は「東南大海中」としていますから、韓国方４千里の対角線を進むコースを考えたのです。 ●　郡から狗邪韓国までは７千里は、方４千里の対角線を歩く距離だとすることを考えました。 ●　方４千里の対角線は５千７００里です。すべて階段状なら８千里になってしまいます。 ●　そこで、階段状の道と直線の道を組み合わせて、方４千里の対角線が７千里になるようにしました。 ●　７千里のうち４千里は碁盤目を行くジグザグ道としました。一辺２千里の方形です。 ●　残り３千里は直線的な道としました。方形は一辺２千１００里の方形です。 ●　この二つを足した４千１００里を方４千里としたのです。７千里が「陸行」になることに注目して下さい。 ●　陳寿は狗邪韓国への行程を【歴韓国乍南乍東】と書いています。通常「乍～乍～」という表現は、上下・左右・東西・緩急・晴雨など反対の語を組み合わせて使います。南と東を組み合わせることはありません。 ●　陳寿が普通では使わない東と南を組み合わせたのは、東南に向かってジグザグに進む有様を表現するためです。　末盧国～不弥国の７百里も「定理」から ●　末盧国～伊都国が５００里、伊都国～奴国は１００里、奴国～不弥国が１００里、合計７００里ですが、この７００里は東南に延びていますから、南北を向く正方形の対角線になります。対角線が７００里になる正方形は一辺が５００里です。このように方５００里は隠されているのです。（付図参照） ●　この４ヵ国、方５００里と壱岐国の方３００里、対馬国の方４００里と合わせて３：４：５になります。 ●　末盧国（唐津市）～伊都国（前原市）は２５キロ、伊都国から奴国（春日市）は３０キロです。 ●　なぜ末盧国～伊都国を５００里としているのに、距離の長い伊都国から奴国を１００里とするのか、すべて方５００里をつくり出すためにつくりだすためのことで、実際の距離とは関係ありません。 ●　７００里の計算でわかるように、距離は累積されています。榎一雄氏のいう放射状ではありません。 ●　また、末盧国から伊都国への方向「東南」について論議がありますが、末盧国から伊都国へはこの対角線を行くのだから「東南」になるのです。この方角は観念上のことで、末盧の海岸で日の出を見て決めた方角ではないのです。 ●　末盧国から伊都国へ「陸行」するとなっていますが、これも前掲のような地図の上でのことだと思います。実際は伊都国まで「水行」していたのでしょう。　不弥国～邪馬台国は√２千里 ●　不弥国まで１万７００里になるから、残りは１千３００余里というこになりますが、それでは面白くありません。 ●　陳寿は全体の「１万２千余里」の「余里」を生かして、√２＝１４１４里をイメージしていたのではないでしょうか。
投馬国について ●「水行二十日」とあるので投馬国は邪馬台国から遠く離れているとされますが、倭人伝の行程は道順に記されています。 ●　この順によれば、不弥国の次が投馬国で、その次が邪馬台国です。 ●　地名を頼りにすると、妻郡とか三潴付近が有力ということになります。 ●　その推理を推し進めていけば、邪馬台国は山門郡ということになりますが、どうでしょうか。 ●　この問題は「水行十日」でとりあげます。　倭人伝にだけ距離が書かれた理由 ●　陳寿が３：４：５にこだわるのは、かれが『九章算術』を読んで【今有勾三尺、股四尺、問為弦幾何？答五尺】の面白さによほど惹かれていたからでしょう。 ●　かれは倭人伝の編纂に際して【其大倭王居邪馬台国、楽浪郡徼、去其国、万二千里、去其西北界狗邪韓国、七千余里】（『後漢書』）という、原史料に書かれた数字「万二千里」が３：４：５という『九章算術』にある数字を含んでいるのに気づき、これから執筆する倭人伝の中で鉤股術（ピタゴラスの定理）を使ってみようと思い立ったのです。 ●　元々「１万２千里（距離不明）」とされ、知る人も少ない倭であれば、いくら数字を作っても問題は起きないと考えたのかもしれません。完成した倭人伝を見る限り、陳寿は数字つくりを存分に楽しんだようです。 ●　『三国志』東夷伝に採り上げた数多い国の中で、なぜ倭人伝だけ細かい距離か書かれているか、どうやらその理由は陳寿の「鉤股術好き」にあるといえそうです。陳寿は歴史家であるだけでなく、算術も大好きな知識人だったのです。
金　印　　水行十日　　韓　国　　邪馬台国　　卑弥呼　　出　口